在考试中,立体几何作为必考题目,解决方法有几何法和向量法两种不同的解法,在考试中主要考查的也仅有八种类型的题目,只要我们将这八种类型全部掌握,就会发现立体几何的题目原来如此简单,竟可以在几分钟之内快速解出来。从今天开始,我会依次将这八种类型用向量法进行详细讲解。今天在视频中和大家分享:如何用向量法求点到面的距离
平面法向量的求法:
(1)设出平面的法向量为$\vec{n}=(x,y,z)$
(2)求出平面内的两个不共线的向量的坐标$\vec{a}=(a_1,a_2,a_3),\vec{b}=(b_1,b_2,b_3)$
(3)根据法向量的定义建立关于x,y,z的方程组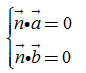
(4)解方程组,取其中的一个解,即取法向量
注:由于一个平面的法向量有无数个,故可在带入方程的解中取一个最简单的作为平面的法向量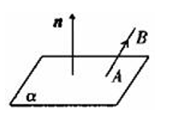

大家课后按照今天的讲解把视频中的练习题做出来,加油!!如有问题请留言,希望大家多多分享,多多转发,谢谢大家。




